Vad är definitionen av en digital och en analog signal?

Rent elektriskt beter de sig som sagt likadant*, men typiskt för digitala signaler är att man till exempel delar upp alla tänkbara spänningar som kan förekomma i "större än x" respektive "mindre än x" och sedan endast bryr sig om klassificeringen. Detta medför, då det till exempel kanske inte spelar så stor roll om spänningen är 1 eller 2 volt, så länge den är under 2,5 (eller var man nu drar gränsen (förmodligen lägre för att få marginal)), i ett 5-voltssystem att digitala kretsar kan tillverkas billigare och uppträda mera robust än analoga (där liknande osäkerheter skulle kunna ackumuleras till större fel).

*Då man som sagt vanligtvis är intresserad av diskreta nivåer kommer förmodligen signaler som förmedlar digital information se ganska typiska ut med snabba omslag mellan två nivåer, men om man skall vara petig blir de aldrig perfekta; elektriska signaler är alltid analoga.

Nja, det är inget jag normalt skryter med. Mera renodlade ljudfrågor hör nog dock bäst hemma i ljud-forumet (jag gissar att audiofiltätheten är större där än här).

Notera att ljud inte kan vara helt digitalt utan måste te sig som en analog signal för att bli just ljud i t ex musiksammanhang.

Däremot finns det teknik som använder en digital signal genom förstärkaren för att generera ett "analogt resultat".

Jag kan starkt rekommendera Christopher "Monty" Montgomerys videor om digitalt och analogt ljud. De är väldigt pedagogiska och dödar en del vanliga myter genom tydliga experiment:

• Del 1 (30 min) — allmänt om digitalisering av analoga kvantiteter i mediasammanhang, med visst fokus på video.

• Del 2 (24 min) — fokus på ljud och vad det innebär för ljudkvalité att representera ljud digitalt med demonstration av Nyquists samplingsteorem.

Videorna är välproducerade och som sagt tydliga.

En signal blir digital när den delas upp i diskreta nivåer med ettor och nollor.

Vi kan ta ett enkelt exempel med en termometer som ger en signal till en dator. En digital signal är då en rad med ettor och nollor som kodar den aktuella temperaturen. Signalen skickas genom att man varierar spänningen med en viss frekvens. Så ett visst antal gånger per sekund mäter man spänningen och är den ett visst värde, säg 5 V så tolkas det som en etta och är den ett annat värde, säg 0 V så tolkas det som en nolla. En typisk analog signal från ett mätinstrument är till exempel en ström på mellan 4 och 20 mA. Då svarar 4 mA mot den lägsta temperaturen i intervallet som termometern mäter och 20 mA motsvarar den högsta temperaturen. Så genom att mäta strömmen så kan man direkt räkna ut temperaturen. Här kan man också använda andra intervall eller så kan man använda spänning istället för ström.

Det låter som att du borde titta på:

http://en.wikipedia.org/wiki/Nyquist%E2%80%93Shannon_sampling...

Av någon anledning tolkar jag det som att du säger emot, tolkar jag dig rätt då?

Men som artikeln di länkar siger:

Digitalt ljud låter inte illa.
Se också videon som phz tipsar om, det bästa och mest lättförståeliga men samtidigt mest detaljerade jag har sett eller läst i ämnet.

(Fortsätter lite på ljudspåret (hoho), iom att det verkar vara det som trådskaparen egentligen var intresserad av.)

Myths (Vinyl) [hydrogenaudio.org] är också en bra wikiartikel som bemöter många "analog vs digital"-felaktigheter, med fokus på just vinyl vs CD.

En viktig poäng är att vissa ibland hävdar att en analog signal teoretiskt är bättre än en digital, eftersom den analoga är en "direkt kopia" (mekanisk/elektrisk/etc.) utav den ursprungliga signalen, medans en digital representation alltid har en viss högsta upplösning. Detta är en logisk felaktighet, för om vi hade tillåtit oss prata om en "teoretiskt perfekt" digital signal för att matcha denna frihet som den analoga metoden nyss fick i tankeexperimentet, dvs en digital signal med oändligt bitdjup, frekvens, etc., så hade den också varit en perfekt representation av originalsignalen. Återigen applicerar Nyquists teorem. Vill man ha ett "matematiskt bevis" för detta så är det bara att läsa några sidor i första bästa litteratur om Fourieranalys; specifikt om Fourierseriers konvergens.

"Men hallå, man kan ju aldrig uppnå en sådan perfekt digital sampling!" — nä, men man kan lika lite uppnå en perfekt analog inspelning. Skillnaden i kvalité på analogt vs digitalt ljud kommer alltid vara en fråga om implementation, och redan CD-standarden från 1980 är storleksordningar bättre i alla mätbara storheter vad gäller objektiv ljudkvalité jfr m i detta fall vinyl. Notera ordet "objektiv", vilket innebär att digital utrustning är bättre på att representera den signal de får given än analog (i motsvarande prisklass). Det är högst fastslaget att digital och analog utrustning låter annorlunda, men om man då väljer att föredra den analoga varianten så är det av ren vana för att man tycker den "låter bättre" utan att riktigt kunna sätta fingret på det, trots att det egentligen representerar en mer förvriden variant av originalet. Lägg därtill bångstyrig nostalgi hos vissa .

Jag minns en kurs på gymnasiet där min lärare drog exakt det där "trappstegsresonemanget" gällande digitala signaler, vilket gjorde att jag trodde på det i flera år, innan jag lärde mig mer om ämnet. Det är ett extremt vanligt missförstånd, och låter vid en första anblick tillräckligt avancerat och tillräckligt rimligt för att det ska fortsätta propagera genom generationer av teknikintresserade. Men det är fel (eller åtminstone ofullständigt).

Jag har sällan känt mig så korkad som när jag faktiskt förstod att det där trappstegsresonemanget bara är trams och såg det bevisat på ett väldigt enkelt sätt.

Och det är ju självklart, det digitala trappsteget vi ser är en representation av en analog vågsignal, det kan inte vara trappsteg!

Samma sak med det argumentet kring halva steg osv, om man har 2 efterföljande digitala punkter med samma värde som är sammankopplade via en vågsignal så kommer vågen ta det halva steget även om dom digitala representationerna inte visar det.
Eller har jag missförstått den biten?

Det är inte helt uppenbart, men det hör långsökt ihop med att den digitala samplingen är bandbreddsbegränsad. Som Monty ritar vid 07:06 i video 2 så skulle man ju kunna tänka sig vilka kringelikrokiga vågformer som helst som skulle kunna passa en viss digital sampling, men i och med att signalen är bandbreddsbegränsad så finns det en unik vågrepresentation (unika koefficienter till Fourierbasfunktioner, om man så vill) som passar under den givna bandbreddsbegränsningen. Vad Nyquist ger oss är att den maximala frekvensen som är representerbar är kopplad till samplingsfrekvensen, där samplingsfrekvensen måste vara mer än dubbelt så stor som våglängden för att den ska kunna representeras (det är en strikt olikhet i gränsen, vilket är viktigt; inte minst för min bild nedan ). 44.1 kHz som på en CD ger att frekvenskomponenter på < 22.05 kHz kan representeras exakt genom de punkter som lagrats. Om man redan i remasterprocessen då "skär av" (bandbreddsbegränsar) ljudet till detta (det är ändå över vad människan kan höra), så kommer den digitala avbilden avforma signalen exakt rätt (bortsett från det kvantiserade bitdjupet, men det gör i praktiken ingen skillnad för örat).

Låt säga att man har två digitala samplade punkter, och det förekommer en frekvenskomponent som "studsar till" precis "mellan" dessa två. Först en implementationsdetalj: en reell samplingsmetod kommer av naturen "integrera" signalen över en kort period vilket gör att punkterna på var sin sida om denna impuls måhända kommer registrera ett högre värde än det exakt momentana värdet. En jämförbar effekt kan man se om man skalar en bild till halva upplösningen med t ex gaussisk interpolation: en vertikal svart linje på vit bakgrund som var en pixel bred i originalupplösningen försvinner i sig, men samplingspunkterna runt omkring påverkas, och man får en gråaktig "rest", där punkterna runt "signalen" har "integrerat" den ursprungliga "impulsen". I praktiken så kan utrustning inte registrera ett perfekt momentant värde precis där samplingsmetoden triggar — stig- och falltid hos utrustning påverkar mätningen. I praktiken kan detta säkert bli "ganska bra", men det är en detalj som kan vara bra att nämna, för att ha en mer praktisk koppling till vad som händer.

Men bortsett från det: en signal som "studsar" till på det sättet skulle beskriva en komponent i frekvensspektrat som var utanför bandbreddsbegränsningen, och därmed inte kunna representeras för den givna samplingsfrekvensen. I fallet vinyl vs CD så skulle denna impuls än mindre kunna representeras på vinylskivan av rent materialtekniska begränsningar, så det är inget "problem", och i och med att CD:n representerar alla frekvenser inom mänsklig hörsel så skulle denna impuls inte ens kunna höras "live". Detta är alltså inget inneboende "analog vs digital"-problem, utan en implementationsdetalj. Det är bra mycket enklare att få bättre allmänna egenskaper hos digital än analog utrustning idag.

Däremot, så bara för att två samplingar i rad i en lång representation är av samma magnitud så betyder inte det att D/A-omvandlaren kommer binda samma dessa med en "rak linje", utan det beror på omgivande punkter. Ett exempel är att tänka sig en vågtopp i en perfekt sinuskurva som råkar hamna symmetriskt mellan två samplingspunkter: den "riktiga" toppen kommer ligga högre än dessa samplingspunkter, men så länge kurvan som beskrivs har en frekvens lägre än Nyquists kriterium så kommer den kunna återskapas perfekt, inklusive sin "kulle" mellan dessa punkter.

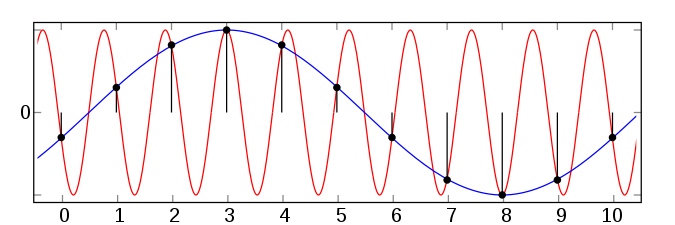
Nyquists gräns är ganska naturlig om man tänker på en ideal sinuskurva: säg att man tar viss mängd samplingar och dessa alla ger värde 0. En möjlig representation av detta är just en "identiskt noll"-signal hela vägen. Men en annan möjlig signal är ju just A sin(π t f), där t är samplingstiden, f samplingsfrekvensen och A en godtycklig amplitud. Denna funktion kommer också vara 0 precis varje gång vi samplar! Därtill kommer alla heltalsmultipler av vinkelargumentet. Försöker mig på en hophackad bild, med sampling varannan tidsenhet och några kurvor inritade:

Alla uppritade signaler i bilden ovan passar in var för sig på mätpunkterna. Eftersom A kunde väljas godtycklig och alla heltalsmultipler av frekvensen också duger så finns det oändligt många signaler som passar in utanför Nyquistkriteriet: det är därför vi måste bandbreddsbegränsa, och vid återskapning säga: "strunta i att försöka passa in signaler över denna frekvens: vi kunde ändå inte fånga upp dem entydigt när vi samplade".

Vad Nyquist också säger, vilket inte är helt uppenbart, är att alla signaler med en frekvens lägre än den högsta kurvan i grafen skulle gå att återskapa exakt med samplingsfrekvensen ovan, och även alla kombinationer av sådana signaler. "Exakt" antar "oändligt" bitdjup, men det är också en implementationsdetalj som inte är en begränsning i Nyquists utsaga. 16 bitar är gott och väl nog för ljud avsett för mänskliga örat.

Om vi inte följer Nyquists råd så får vi så kallad aliasing (på ett datorforum så känner många säkert till begreppet "anti-aliasing"). Alla kurvor i bilden ovan är exempel på aliaskurvor, dvs kurvor som alla passar in på en viss sampling. Den länkade Wikipediaartikeln har en alternativ bild för samma sak, där både blå och röd signal skulle passa in på givna datapunkter (där röd alltså är bortom Nyquists gräns):

Jag slutar här. Kom på alldeles nyss att man kanske borde börjat med Fouriers försäkran om att man kan bygga upp vilken funktion som helst (nåja) utifrån dess oscillerande frekvenskomponenter (då dessa bildar en fullständig bas). Någonstans i textkaskaden fanns kanske svaret på frågan, och troligen mycket som inte var direkt relevant till just denna . Trots att det var många ord så är det långt ifrån fullständigt, men förhoppningsvis inte rent av felaktigt (åtminstone inte så att min förmåga kan upptäcka det).

Haha, jo, kul att du utvecklade även om det känns om på gränsen till vad jag klarar av att ta till mig just nu.

Sen angående ditt bildexempel tidigt i texten så kommer jag och tänka på ett kul exempel från ett video encoder test jag läste där dom jämförde lite olika bitrates och codecs.
Det var en scen ifrån någon av Matrix filmerna har jag för mig där bakgrunden var vitt kakel och såg ut typ så här:

Med vissa codecs i vissa bitrates så blev det dock helt vitt och såg ut som en helt vanlig vit vägg, första gången jag insåg vilken påverkan många codecs har även om filmen nästan ser dvd-skarp ut i övrigt...