5D MkII
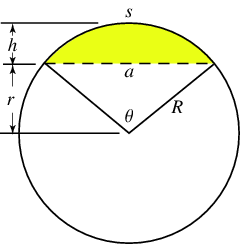
Avstånd linje-cirkelsegment
Visa signatur
Visa signatur
Min hemsida: http://www.srekel.net
Pocket Task Force: http://ptf.srekel.net
Kaka e gott! http://kaka.srekel.net
Visa signatur
5D MkII
Visa signatur
...man is not free unless government is limited. There's a clear cause and effect here that is as neat and predictable as a law of physics: As government expands, liberty contracts.
Visa signatur
5D MkII
Senast redigerat
Visa signatur
:€